Konstruktion eines Hyperwürfels - Grundlagen
Die meisten von uns wissen, dass unser Gehirn bei Hyperräumen abschaltet. Warum gibt es dennoch so viele Überlegungen dazu? Woher kommen die ganzen Gedankengänge und Spielereien zu diesem Thema? Man muss unterscheiden: Wir können uns einen 4D-Raum direkt zwar nicht vorstellen, mit bestimmten Tricks lassen sich aber dennoch interessante Überlegungen dazu anstellen, mehr dazu weiter unten. Allgemein kann man zuerst mal sagen: Um ein Objekt auf die nächst höhere Dimension zu bringen, muss man es senkrecht zu sich selbst verschieben, kurz gesagt auseinanderziehen (siehe Bild rechts). Um zu verstehen wie das gemeint ist, wird nun im Folgenden ein vierdimensionaler Hyperwürfel auseinander genommen. Oder zusammengebaut, ganz wie Sie wollen. |
|
 |
Pinselei: Um ein Objekt auf die nächst höhere Dimension zu bringen, muss man es "auseinanderziehen". Beispiel: Aus einem Farbklecks (0D) wird ein Pinselstrich (1D). Im Prinzip verläuft das komplette Konstruktionsverfahren höherdimensionaler Objekte nach diesem Prinzip. |
|
|
Teil 1: Die Ecken eines Hyperwürfels
Viele der Tricks, sich höherdimensionale Gebilde vorzustellen, beruhen auf Vergleichen: Man schaut z.B. zuerst mal, was beim Übergang von der 2. auf die 3. Dimension passiert und überträgt das Ganze dann auf den Sprung von der dritten in die vierte Dimension. Kleines Beispiel: Ich würde gerne wissen, wieviele Ecken ein vierdimensionaler Würfel hat. Unmöglich sich ein solches Gebilde vorzustellen, aber jetzt kommt der Trick: Erweitert man ein Quadrat (2D,
vier
Ecken) zu einem Würfel (3D, 8 Ecken), sieht man, dass sich die Anzahl der Ecken verdoppelt hat. Denn beim "Auseinanderziehen" des Quadrats bleiben ja die 4 alten Ecken stehen und 4 neue bilden sich auf der gegenüberliegenden Seite. Das Gleiche passiert nun auch bei der Erweiterung des 3D-Würfels auf den vierdimensionalen Hyperwürfel: Die alten Ecken bleiben stehen, und in der neuen Dimension steht jeder alten Ecke eine neue Gegenüber, der Hyperwürfel hat also 16 Ecken. |
|
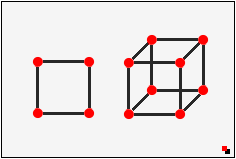 |
Quadratur des Quadrates: Erweitert man ein Quadrat zu einem Würfel, verdoppeln sich die Ecken. Die "alten" Ecken bleiben stehen, und in der neuen Dimension stehen diesen alten Ecken nun ebenso viele neue gegenüber. Wie ein Spiegel. |
|
|
Teil 2 - Die Kanten
Eine Kante entsteht beim Auseinanderziehen einer Ecke. Zur Gedankenstütze hier nochmal kurz das Beispiel mit dem Pinsel (siehe Bild oben): Man könnte sagen, der Farbfleck mit seinen null Dimensionen entspricht einer Würfelecke (auch null-dimensional), und der Pinselstrich steht für eine Würfelkante (beides hat eine Dimension). Also wieder zurück zu den Kanten. Das Quadrat hat 4 davon. Wenn man es auseinanderzieht entsteht wie gewohnt auf der gegenüberliegenden Seite ein neues Quadrat, macht also erstmal 8 Kanten. Aus jeder der 4 Ecken des Quadrats entsteht jetzt aber noch zusätzlich, denken Sie an den Pinsel eben, eine neue Kante. Macht also insgesamt 12 Kanten beim 3D-Würfel. Stimmt's? Zählen Sie beim nächsten Kniffel mal nach. Nun die gehen wir zu den Kanten des Hyperwürfels: 12 Kanten vom alten plus 12 vom gegenüberliegenden 3D-Würfel macht 24, und jede der 8 Ecken des 3D-Würfels wird beim Hyperwürfel zu einer Kante, ergibt stolze 32 Kanten. Es ist übrigens keine Schande diesen Text 2 mal zu lesen. |
|
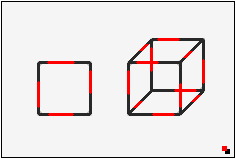 |
Warum hat ein 3D-Würfel 12 Kanten? Ganz einfach: 4 vom Ursprungsquadrat, 4 von dessen Spiegelung, und 4 weitere entstehen durch das Auseinanderziehen der 4 Ecken. |
|
|
|
Teil 3 - Die Flächen
Ecken und Kanten haben wir also im Griff. Nun sind die Flächen an der Reihe: Der 3D-Würfel hat 6 davon, aber wieviel gibt’s beim Hyperwürfel? Dazu schauen wir wieder zurück was eine Dimension tiefer passiert: Beim Auseinanderziehen des Quadrats zum Würfel bleibt die ursprüngliche Fläche stehen und auf der gegenüberliegenden Seite bildet sich eine neue. Aber das war's noch nicht ganz, dazwischen sind ja nochmal 4 entstanden, diese kommen von den 4 Kanten des Quadrats. Somit haben wir also die bekannten 6 Flächen gefunden. Nun das Ganze in 4D: Auch beim Erweitern des 3D-Würfels bleibt der ursprüngliche Würfel erstmal stehen und gegenüber bildet sich ein neuer, wobei sich dieses Gegenüber jetzt schon in der vierten Dimension befindet. Wir erhalten also schonmal 12 Flächen aus altem und neuem Würfel. Und was passiert dazwischen? Jede der 12 Kanten des ursprünglichen 3D-Würfels wird beim Auseinanderziehen zu einer Fläche erweitert. Das bedeutet wir haben 12+12=24 Flächen auf dem 4D-Hyperwürfel. |
|
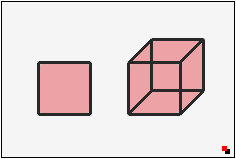 |
Erweitert man ein Quadrat zu einem Würfel, erhält man 5 neue Seitenflächen. Eine davon kommt von der "Spiegelung", und 4 entstehen durch die senkrechte Verschiebung der 4 Kanten des Quadrates. |
|
|
|
Das endgültige Aussehen des 4D-Hyperwürfels
Ein Hypercube hat also 16 Ecken, 24 Seitenflächen und 32 Kanten. Das Interessanteste kommt aber noch: Von was wird denn der Hypercube außen abgegrenzt? Und jetzt nutzen wir den kleinen Trick mit den Dimensionssprüngen schamlos aus: Eine eindimensionale Gerade wird von zwei nulldimensionalen Punkten abgegrenzt, auf deutsch die Wurst hat zwei Enden. Ein zweidimensionales Quadrat wird von 4 eindimensionalen Geraden abgegrenzt. Und ein dreidimensionaler Würfel wird von 6 zweidimensionalen Seitenflächen umschlossen. Die eingrenzenden Objekte haben also immer eine Dimension weniger als das Objekt selbst. Das bedeutet, dass der 4D-Hypercube von dreidimensionalen Objekten eingezäunt wird. Ist das für den Abschluss nicht eine schöne unvorstellbare Vorstellung? Es sind übrigens 8, soviel Zeit muss sein. |
|
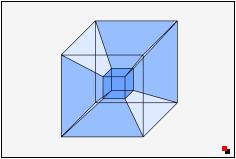 |
Jeder Versuch, einen 4D-Hyperwürfel auf einer 2D-Oberfläche darzustellen, geht grundsätzlich in die Hose. Es sind bestenfalls pseudoartige Projektionen möglich, die einen kleinen Eindruck von seiner Komplexität vermitteln. Die hier gezeigte Darstellung gibt immerhin die Anzahl der Ecken, Kanten und Flächen korrekt wieder. |
|
|
| |
| << zurück | 1 | 2 | 3 | 4 | weiter >> |
| |
| Mehr Physik auf drillingsraum.de |
|
| |
| Home | Impressum | Contact | Physik | Physik-Forum | Sitemap |
| |
| |